
See Example 4.26 through Example 4.34.Ĭopyright © SAS Institute, Inc. When the pattern is linear, you can use Q-Q plots to estimate shape, location, and scale parameters and to estimate percentiles.
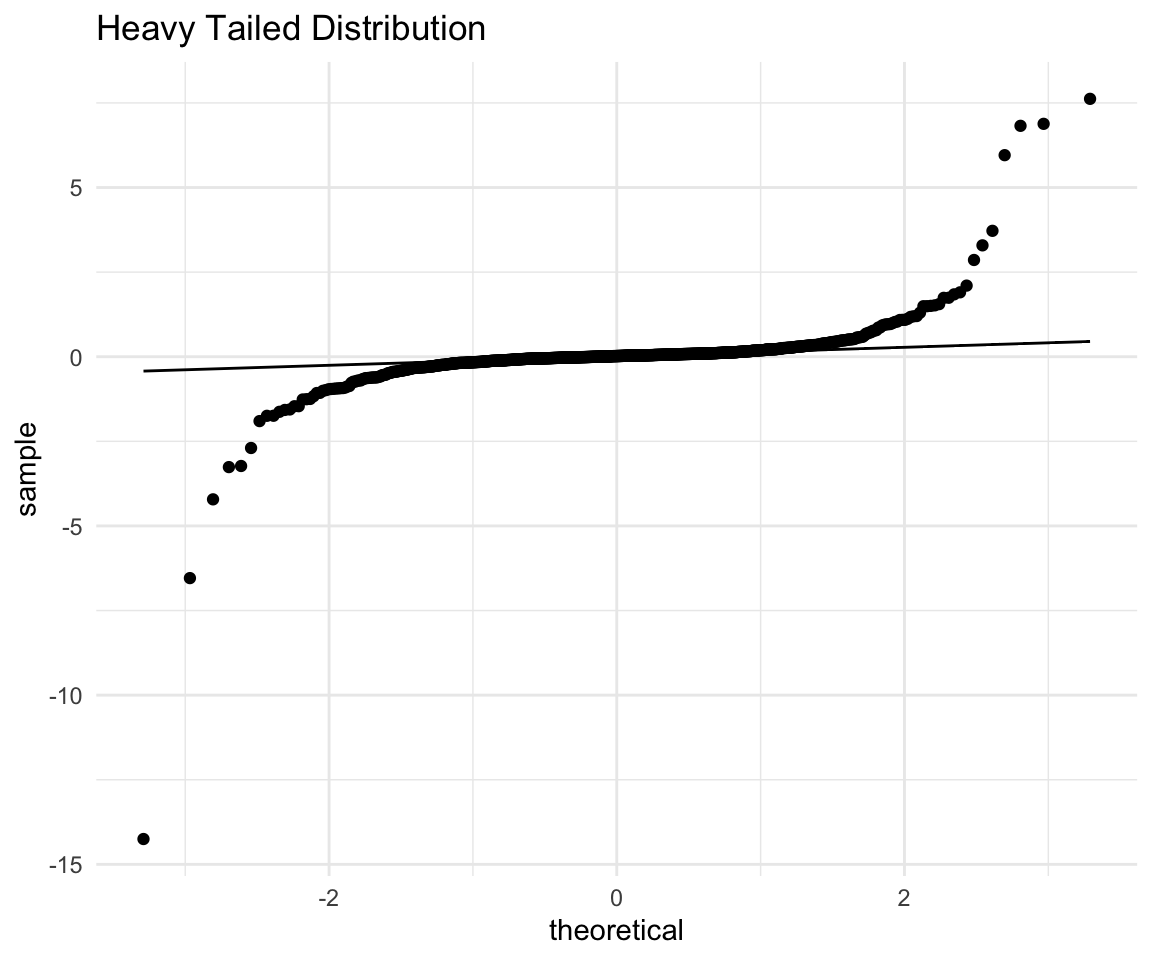
Short tails at both ends of the data distributionĬurved pattern with slope increasing from left to rightĬurved pattern with slope decreasing from left to right Left end of pattern is above the line right end of pattern is below the line Long tails at both ends of the data distribution Left end of pattern is below the line right end of pattern is above the line Pretty big impact The four plots show potential problematic cases with the row numbers of the data in the dataset. If I exclude the 49th case from the analysis, the slope coefficient changes from 2.14 to 2.68 and R 2 from. Table 4.85 Quantile-Quantile Plot Diagnostics The plot identified the influential observation as 49. ( 1983) note that departures from linearity can also be due to chance variation. In some applications, a nonlinear pattern may be more revealing than a linear pattern. ( 1983) and Fowlkes ( 1987) discuss the interpretations of commonly encountered departures from linearity, and these are summarized in Table 4.85. There are many reasons why the point pattern in a Q-Q plot may not be linear. On the other hand, probability plots are more convenient for estimating percentiles or probabilities. Q-Q plots are more convenient than probability plots for graphical estimation of the location and scale parameters because the -axis of a Q-Q plot is scaled linearly. The slope and intercept are visual estimates of the scale and location parameters of the theoretical distribution. and coauthor of the Stata Press book Flexible Parametric Survival Analysis Using. If the theoretical and data distributions differ only in their location or scale, the points on the plot fall on or near the line. Options for symplot, quantile, and qqplot. If the quantiles of the theoretical and data distributions agree, the plotted points fall on or near the line. On a Q-Q plot normally distributed data appears as roughly a straight line (although the ends of the Q-Q plot often start to deviate from the straight line). The normal distribution is symmetric, so it has no skew (the mean is equal to the median). The following properties of Q-Q plots and probability plots make them useful diagnostics of how well a specified theoretical distribution fits a set of measurements: Below is an example of data (150 observations) that are drawn from a normal distribution. Interpretation of Quantile-Quantile and Probability Plots


 0 kommentar(er)
0 kommentar(er)
